Research
情報理論
ランダム行列・自由確率・漸近幾何解析と量子情報及び深層学習
![]()
数学と情報理論の学際分野で研究
数理科学分野 福田素久 教授
情報理論は他分野との関連も多く、例えば統計力学とはエントロピーの概念を共有しています。情報理論の一分野である通信理論はシャノンによって確立され、そこでは通信の効率性の定式化が行われました。現在の通信工学はこのシャノンの通信理論の上に成り立っているといえます。しかし、量子物理的効果が生じる量子通信ではこの理論は成り立たず、その定式化が望まれます。本研究室では、このような量子通信に特有の性質を、ランダム行列・自由確率・漸近幾何解析等を用いて研究してきました。現在はこれらの研究手法を用いて深層学習の研究を開始し、実践的な応用研究も他分野の研究者と始めました。
研究手法
ランダム行列とは行列の要素が確率変数となっている行列で、主に固有値の分布などが研究されています。この解析的な問題を、行列のサイズが大きい極限を考えて、代数確率空間で扱うのが自由確率です。また、漸近幾何解析の分野からは高次元空間での確率論を用いています。複雑な現象も、高次元やその極限では見通しが良くなることがあります。
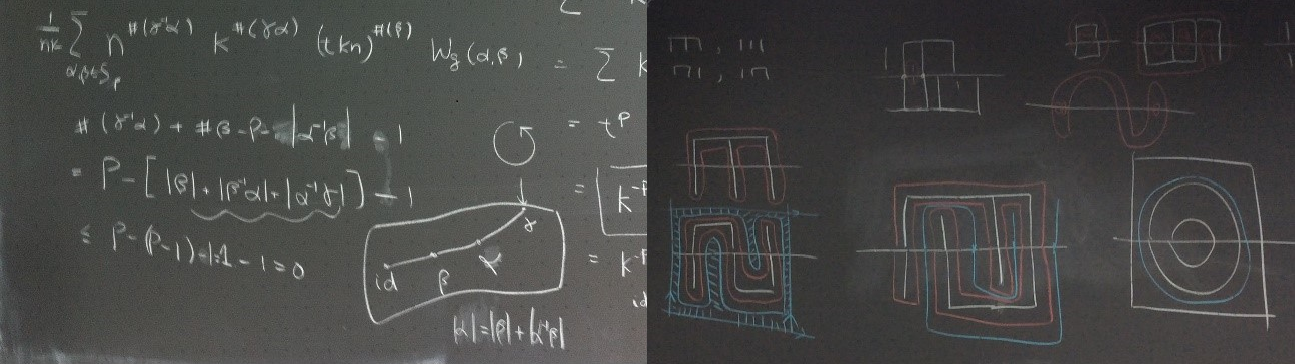
数学の議論は黒板やホワイトボード等を使用する。写真はIon Nechita (トゥールーズ大学)と行った議論の記録の一部。
量子通信
量子物理によって記述された通信モデルは、ユニタリ行列によって記述できるため、ランダムなユニタリ行列によって生成された量子通信路を考察することで、高次元での量子通信路の典型的な振る舞いを研究しています。ここで、ユニタリ行列とは空間の回転を記述する行列でその要素が一般に複素数となります。
プログラム
ランダムなユニタリ行列の平均の計算式は組み合わせ論を用いて記述されるため、その計算式をプログラムとして書きました。今後はこのプログラムの拡張や応用範囲の拡大を目指しています。
深層学習
上記の研究手法を拡張して深層学習の理論研究を開始しました。また、実践研究ではいくつかのプロジェクトが進行中ですが、最初の研究成果として奥野研究室との共同研究で画像による果実のサイズ測定があります。

ナシの大きさを画像のピクセルとして計測。右はニューラルネットワークが中心にあるナシを認識したところ。
